数学をもう一度・・・

「関数」と言われると数学の教科書に書かれている
\[y=2x,~~ y=-\frac{1}{2}x+3,~~\cdots\]
などの数式を思い浮かべるかもしれない．確かに、中学や高校で学習する数学の関数は、数式で表されたものである． では、「関数」で大切なことは、数式で表すことなのだろうか？
「関数」は「対応」を表しているという捉え方が大切である．
例えば、コンビニでア社のポテトチップスを買うとしよう．そのポテトチップスに円という価格がつけられていれば、

ア社のポテトチップス → 98円

という対応を考えることができる．
このコンビニエンスストアのその時点でア社のポテトチップスの価格は、98円以外には存在しない．
他のメーカーのポテトチップス

イ社のポテトチップス → 105円
ウ社のポテトチップス → 98円

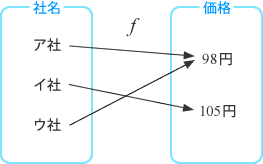
があったとすると、対応は、

図．会社と価格の対応関係

のように→で対応づけることができる．このときの矢印 \( f \) を関数という．
このように、あるものAを決めたとき、それに対応するものBが一つ決まるとき「AをBの関数」という．
このような2つのものA,Bについての関係は、商品と価格以外にもいろいろ考えられる．　身の回りの関数を探してみよう．
ここからは、単純に数字と数字の関係について扱うことにする．

教科書には，「関数」と書いてあるが，「関数」はどういう意味があるのか？

古い教科書を見ると「関数」は，「函数」と書いてある。　「函数」は中国語で発音すると英語の”function”に似ている。「幾何」と同様に「函数」も音から中国に入ってきた言葉といわれている。日本では「函数」を教科書に記載するとき，常用漢字に「函」が含まれないことから，「数と数の関係を表す意味」と捉えて，「関数」と記述した。

“function” を辞書で調べて見よう。　どのような意味が載っているだろうか？

「人やものがおこなう特別な活動や目的」という概念を表す言葉で，「機能」, 「作用」, 「働き」

などが書かれている。

\( x \) についての等式
\[ a_n x^n + \cdots + a_1 x + a_0 = b_n x^n + \cdots + b_1 x + b_0\]
が，\( x \) について恒等式であるならば，
\begin{eqnarray*}
a_n &=& b_n \\
&\vdots& \\
a_2 &=& b_2 \\
a_1 &=& b_1 \\
a_0 &=& b_0
\end{eqnarray*}
となる．

逆に
\( x \) についての等式
\[ a_n x^n + \cdots + a_1 x + a_0 = b_n x^n + \cdots + b_1 x + b_0\]
において
\begin{eqnarray*}
a_n &=& b_n \\
&\vdots& \\
a_2 &=& b_2 \\
a_1 &=& b_1 \\
a_0 &=& b_0
\end{eqnarray*}
ならば，
\[ a_n x^n + \cdots + a_1 x + a_0 = b_n x^n + \cdots + b_1 x + b_0\]
は\( x \) について恒等式となる．

\( x \) についての等式
\[ a_n x^n + a_{n-1} x^{n-1} + \cdots + a_2 x^2 + a_1 x + a_0 = 0\]
が，\( x \) について恒等式であるならば，
\[ a_n = a_{n-1} = \cdots a_2 = a_1 = a_0 =0 \]
となる．
逆に
\( x \) についての等式
\[ a_n x^n + a_{n-1} x^{n-1} + \cdots + a_2 x^2 + a_1 x + a_0 = 0\]
において
\[ a_n = a_{n-1} = \cdots a_2 = a_1 = a_0 =0 \]
ならば，
\[ a_n x^n + a_{n-1} x^{n-1} + \cdots + a_2 x^2 + a_1 x + a_0 = 0\]
は\( x \) について恒等式となる．

文字\( x \) を含む等式において，\( x \) にどのような値を代入しても両辺の値が等しくなる式を\( x \)についての恒等式(Identical equations)という．

換言すると，「任意の\(x\)に対して成り立つ等式を恒等式という」

文字\( x \) を含む等式において，その等式が，\(x\)について恒等式でないならば，
その等式を\( x \)についての方程式(Equations)という．
また，等号が成り立つときの\(x\) の値をその方程式の解(Solution)という．

換言すると，「特定の\(x\)に対して成り立つ等式を方程式という」

多項式の計算において，\( x \) や \( y \) などの文字は，特に意味は無く未知数を扱うための文字を用いた一つの表現(expression：式)に過ぎない．
例えば，未知数\( x \)がどのような値を取るかわからないが（任意の\(x\)について），
\[2x^3+x^2-x+1\]
と表現された式があるとする． もし，\( x \) が \(2\) であれば，\( x \)の代わりに\( 2 \) を書いて，
\[ 2 \cdot 2^3 + 2^2\ – 2 +1 = 19 \]
となる． このように，文字 \( x \) を \( 2 \) に置き換えることを，
式に値を代入するといい，その代入した結果の値を式の値という．

（例）\( x=-2 \) のとき，式 \( x^2 – x^3 \) の値を求めよ．
\[ x^2 – x^3 = (-2)^2 – (-2)^3 = 4-(-8) = 4+8 = 12\]

（例）\( x=123,~y=122 \) のとき，式 \( x^2 – y^2 \) の値を求めよ．
\[ x^2 – y^2 = (x+y)(x-y)=(123+122)(123-122)=145 \cdot 1 = 145\]

多項式と多項式の積も，分配法則を利用すれば，単項式と単項式の計算となる．
例えば，
\[ (x^2 + y^3)( x + y^2 )\]
は，
\begin{eqnarray*}
\color{red}{(x^2 + y^3)}( x + y^2 ) & = & \color{red}{(x^2 + y^3)} x + \color{red}{(x^2 + y^3)}y^2\\
& = & x^3 + xy^3 + x^2y^2 + y^5 \\
& = & x^3 + x^2y^2 + xy^3 + y^5
\end{eqnarray*}
となる．

(注)
\( A=(x^2 + y^3) \)とおけば，分配法則より\(A( x + y^2 )=Ax+Ay^2\)となる．
\( A \) を元に戻せば，\( (x^2 + y^3)x +(x^2 + y^3)y^2 \)が得られる．

単項式と多項式の積は，分配法則を利用すれば，単項式と単項式の計算となる．
例えば，
\[ x^2y^3( x + y^2 )\]
は，
\begin{eqnarray*}
x^2y^3( x + y^2 ) & = & (x^2y^3) \times x + (x^2y^3) \times y^2 \\
& = & x^3 y^3 + x^2 y^5
\end{eqnarray*}
となる．

単項式と単項式の積は，交換法則と指数法則を利用する．
例えば，
\[ (x^2y^3) \times ( x y^2 )^3\]
は，
\begin{eqnarray*}
(x^2y^3) \times ( x y^2 )^3 & = & (x^2 \times y^3) \times ( x^{1 \times 3} \times y^{2 \times 3} ) \\
& = & x^2 \times y^3 \times x^3 \times y^6 \\
& = & x^2 \times x^3 \times y^3 \times y^6 \\
& = & x^{2 + 3} \times y^{3 + 6} \\
& = & x^5 y^9 \\
\end{eqnarray*}
となる．

1. \( x^2 \times x^3 = (x \times x ) \times (x \times x \times x ) = x^5 (=x^{2+3}) \)
2. \( \big(x^3\big)^2 = (x \times x \times x ) \times (x \times x \times x ) = x^6 (=x^{3 \times 2}) \)
3. \( \big(x y\big)^2 = (x \times y) \times (x \times y ) = x \times y \times x \times y = x \times x \times y \times y = x^2y^2 \)

一般に，\( m,~n \) を整数としたとき，

1. \( x^m \times x^n = x^{m+n} \)
2. \( \big(x^m\big)^n = x^{m n} \)
3. \( \big(x y\big)^m = x^m y^m \)

が成り立つ．これを指数法則という．

また，\( x \ne 0 \)のとき，\( x^0 = 1 \) とし，\( p \)を正の整数とするとき，\( p^{-1} = \frac{1}{p} \)と定義する．