数学をもう一度・・・

1次関数とは

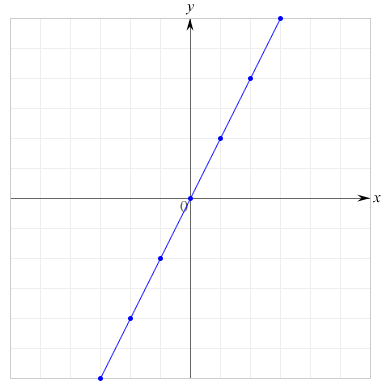
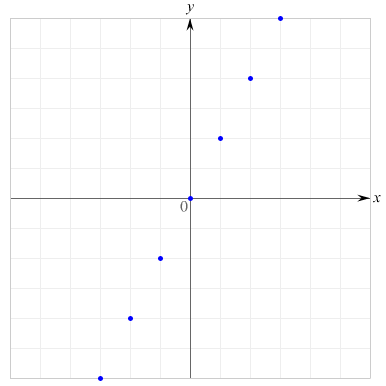
一般に\(a\), \(b\) を定数としたとき，\(y\)が\(x\)の一次式\( y = ax + b\)で表されるとき，すなわち，\(y\)が\(x\)の一次式で表されるとき，\(y\)は\(x\)の一次関数であるといいます．

　

いろいろな比例のグラフを描こう

\(y= ax \)の\(a\)の値を変更して，いろいろなグラフを描こう[Firefox 14.0, Safari 5.1 の動作確認済].

気づいたことは，メモしておこう．

比例のグラフと傾き

プロットした全ての点は一直線上に並ぶ．

比例のグラフの例

この\(y=2x\)の式において，\(x\)の係数2は，\(x\)が1増加すると\(y\)が2増加することを表している．
\(x\)の係数2は，グラフを観てわかるように，グラフの傾きを表しているので，2のことを直線\(y=2x\)の傾きという．

点のプロット

\(y=2x\)のグラフを例に比例のグラフを考える．まず，\(x,~y\)の関係を表にする．

\(x\)	-3	-2	-1	0	1	2	3
\(y\)	-6	-4	-2	0	2	4	6

この表から(\(x\),\(y\))のペアを考える．

\[ (-3,~-6) , (-2,~-4) , (-1,~-2) , (0,~0) , (1,~2) , (2,~4) , (3,~6)\]

このペアを座標と考えて，座標平面上に点をとりましましょう．

このように，座標平面上に点をとることを「点をプロットする」といいます．

座標平面と座標

比例のグラフを考える．グラフを描くために，次のようなものを導入する．

これを座標平面という．横の数直線を\(x\)軸，縦の数直線を\(y\)軸という．\(x\)軸と\(y\)軸の交点を原点といい，Oで表す(OはOriginの頭文字)．
座標平面上の点PをP(3,5)と表す．この(3,5)を座標といい，3を\(x\)座標，5を\(y\)座標という．

比例を\(x\)と\(y\)の式で表す

次に\(x\),　\( y \)を使って表してみよう．「支払った金額」を\( y \)[円]，「買った菓子の個数」を \( x \) [個] とする．そうすると

（支払った金額）＝200×（買った菓子の個数）

は，

\[ y = 200 \times x\]

と表すことができる．　このように“\(y\) =（\( x \)の式）”で表すことを「\( y \) を \( x \) の式で表す」という．

一般に，定数\( a \) を使って，

\[y = a x\]

の式の形で表されるとき，\( y \) は \( x \)に比例するといい，\(a \) を比例定数という．\(a\) は \(x \) が1増加したときの\( y \)の増加する量を表している．

比例を式で表す

買った個数と支払った金額を表にして考えると

買った菓子の個数（個）	1	2	3	4	5	6	7
支払った金額（円）	200	400	600	800	1000	1200	1400

さて，買った個数と支払った金額の関係（対応）を考えてみよう．

買った菓子の個数（個）	1	2	3	4	5	6	7
\(f\)
支払った金額（円）	200	400	600	800	1000	1200	1400

どのような関係があるだろう．

買った菓子の個数（個）	1	2	3	4	5	6	7
\(f\)
支払った金額（円）	200	400	600	800	1000	1200	1400

支払った金額は菓子の個数を200倍することで求められることがわかりる．
式で表すと

（支払った金額）＝200×（買った菓子の個数）

のようになる．
このような式で表されるとき，「支払った金額」は「買った菓子の個数」に比例するといいます．当然，これも「支払った金額」は「買った菓子の個数」の関数です．

比例

最も簡単だけれども美しい性質をもつ関数「比例」について学習しよう．
早速，「比例」って何かを考えてみよう．

例えば，一袋200円の菓子を

1つ買うと200円．
2つ買うと400円．
3つ買うと600円．

このように，買った個数と支払った金額を表にして考えると

買った菓子の個数（個）	1	2	3	4	5	6	7
支払った金額（円）	200	400	600	800	1000	1200	1400

では，買った個数と支払った金額の関係（対応）を「買った菓子の個数（個）」と「支払った金額（円）」の比に注目して考えてみる．

（支払った金額）：（買った菓子の個数）＝２００：１＝４００：２＝・・・＝１４００：７

となって，（支払った金額）の（買った菓子の個数）に対する比の値は，つねに

\[ \frac{200}{1}=\frac{400}{2}= \cdots = \frac{1400}{7} \]
となり，一定の値\(200\)となる．このように，「（支払った金額）の（買った菓子の個数）に対する比の値が一定」となるとき，「（支払った金額）は（買った菓子の個数）に比例する」という．

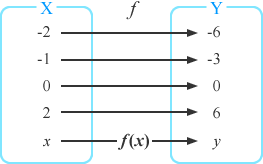
\( y \) が \( x \)の関数とは

関数とは2つのともなって変わる数 \( x \), \( y \) があって， \( x \)の値を一つ決めると，それに対応する\( y \) の値がただ1つと定まるとき、\( y \) を \( x \) の関数といい、

\[ y = f(x) \]

と表す．
また，ともなって変わる数 \( x \), \( y \) のことを変数といい，特に\( y \) を従属変数， \( x \)を独立変数という．

ともなって変わる量

次のような、XとYの対応 \(f\) を考える．

図．ともなって変わる量

XとYはどの\( f \) ような対応になっているか考えてみよう．

Xの中の \(x\) は \(f\) によって \(y\) に対応している．このことを、

\[ y=f(x) \]

と表す．

では，\( f \) にはどのような機能(Function)があるのか？

図を見ると、「2倍する」という機能だといえる．
だから、\( x \) は \( f \) という機能によって、2倍され\( 2x \) となるので、

\[ f(x) = 2x \]

となる (→参照 )．　また、\( y = f(x) \) だから

\begin{eqnarray*}
y &=& f(x) \\
&=& 2x
\end{eqnarray*}

即ち，

\[ y=2x \]

と表すことができる．

数学をもう一度・・・