2次関数の基本形\( y=ax^2 ( a>0, x \in \mathbb{R})\)における\(y\)の最大値と最小値
は、
最小値:\(y=0\) \( (x=0 ) \)、 最大値:なし
である。
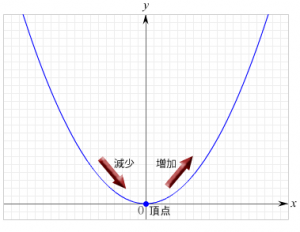
なぜなら、下図のように、\( x \)が、実数全体(\(x \in \mathbb{R}\))の値を取る場合、減少から増加に転ずる点が、頂点\( ( 0, 0 ) \)となるからである。よって、頂点の\(x\)座標、\(y\)座標から、\( x=0 \) のとき最小値\( y= 0 \)をとる。
一方、最大値はグラフが無限に上方に伸びている。
換言すると、\( x \)、\( y \)の値は、\( x \)が小さくなればなるほど、\( y \)も限りなく大きくなる。そのため、\( x \)最大値は存在しない。
同様に\( x>0 \)において、\( y \)の値は、\( x \)が大きくなればなるほど、\( y \)も限りなく大きくなる。そのため、\( x>0 \)において\( y \)の最大値は存在しない。