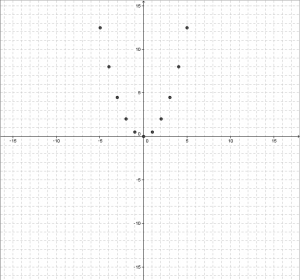
下のグラフから座標平面上に点をプロットしてみよう。
| \(x\) | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(y\) | \( 18 \) | \(\frac{25}{2}\) | \( 8 \) | \(\frac{9}{2}\) | \( 2 \) | \(\frac{1}{2}\) | 0 | \(\frac{1}{2}\) | \( 2 \) | \(\frac{9}{2}\) | \( 8 \) | \(\frac{25}{2}\) | \( 18 \) |
の \(x, y \)のペアを座標平面上にプロットすると、下図のようになる。