数学をもう一度・・・

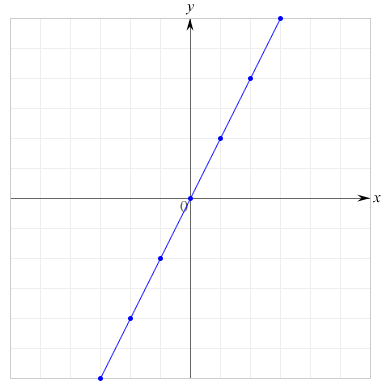
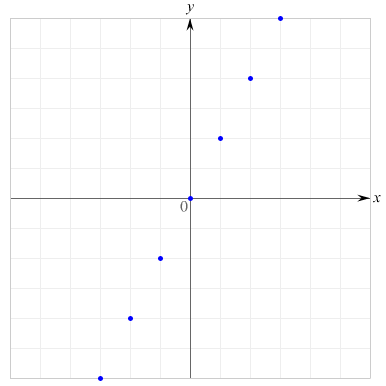
一般に\(a\), \(b\) を定数としたとき，\(y\)が\(x\)の一次式\( y = ax + b\)で表されるとき，すなわち，\(y\)が\(x\)の一次式で表されるとき，\(y\)は\(x\)の一次関数であるといいます．

　

\(y= ax \)の\(a\)の値を変更して，いろいろなグラフを描こう[Firefox 14.0, Safari 5.1 の動作確認済].

気づいたことは，メモしておこう．

プロットした全ての点は一直線上に並ぶ．

比例のグラフの例

この\(y=2x\)の式において，\(x\)の係数2は，\(x\)が1増加すると\(y\)が2増加することを表している．
\(x\)の係数2は，グラフを観てわかるように，グラフの傾きを表しているので，2のことを直線\(y=2x\)の傾きという．

\(y=2x\)のグラフを例に比例のグラフを考える．まず，\(x,~y\)の関係を表にする．

この表から(\(x\),\(y\))のペアを考える．

\[ (-3,~-6) , (-2,~-4) , (-1,~-2) , (0,~0) , (1,~2) , (2,~4) , (3,~6)\]

このペアを座標と考えて，座標平面上に点をとりましましょう．

このように，座標平面上に点をとることを「点をプロットする」といいます．

比例のグラフを考える．グラフを描くために，次のようなものを導入する．

これを座標平面という．横の数直線を\(x\)軸，縦の数直線を\(y\)軸という．\(x\)軸と\(y\)軸の交点を原点といい，Oで表す(OはOriginの頭文字)．
座標平面上の点PをP(3,5)と表す．この(3,5)を座標といい，3を\(x\)座標，5を\(y\)座標という．