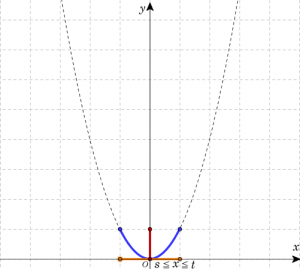
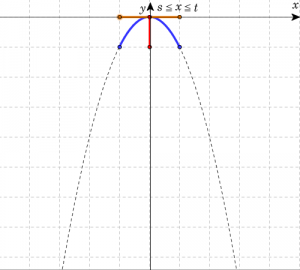
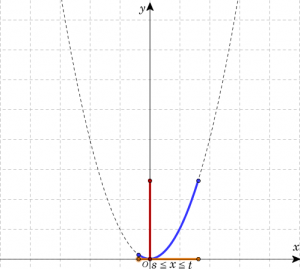
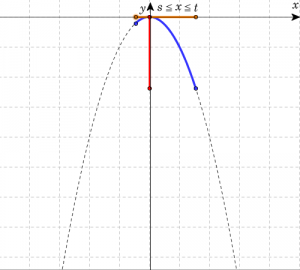
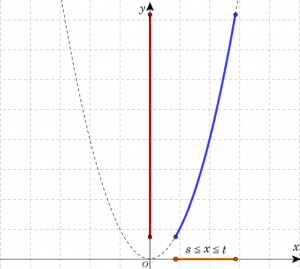
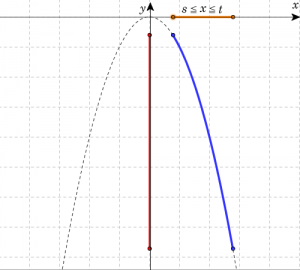
\( s < t \)として、定義域が \( s \leqq x \leqq t \)における２次関数 \(y=ax^2\) の最大値と最小値を以下の表にまとめる。定義域に頂点を含む場合、下図における（真ん中の3つの表の）定義域を表す黄色い線分の中点に注目すればよい。
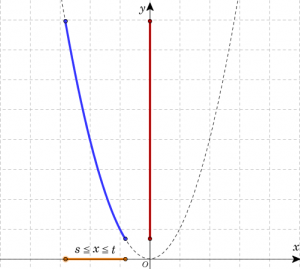
| \( t \leqq 0 \)のとき（\(x\)の取り得る値が負の場合） | ||
| \(a\)の値 | \( a>0 \) | \( a<0 \) |
| 最大値 | \(s^2\) (\(x=s\)) | \(t^2\) (\(x=t\)) |
| 最小値 | \(t^2\) (\(x=t\)) | \(s^2\) (\(x=s\)) |
| グラフ |
 下に凸の放物線の最大値と最小値(\(x\)の取り得る値が負の場合) |
 上に凸の放物線の最大値と最小値(\(x\)の取り得る値が負の場合) |
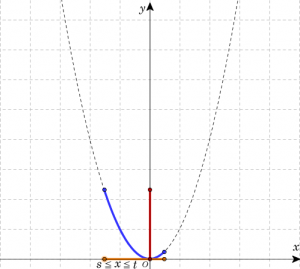
| \(\frac{t+s}{2}<0\)のとき （\(x\)の取り得る値範囲に頂点を含む場合) | ||
| \(a\)の値 | \( a>0 \) | \( a<0 \) |
| 最大値 | \(s^2\) (\(x=s\)) | \(0\) (\(x=0\)) |
| 最小値 | \(0\) (\(x=0\)) | \(s^2\) (\(x=s\)) |
| グラフ |
 下に凸の放物線の最大値と最小値(\(x\)の取り得る値範囲に頂点を含む場合) |
 上に凸の放物線の最大値と最小値(\(x\)の取り得る値範囲に頂点を含む場合) |
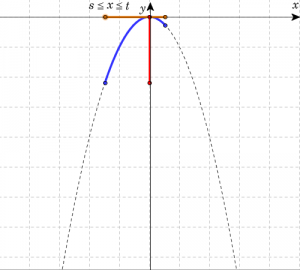
| \(\frac{t+s}{2}=0\)のとき （\(x\)の取り得る値範囲に頂点を含みグラフが対称となる場合） | ||
| \(a\)の値 | \( a>0 \) | \( a<0 \) |
| 最大値 | \(s^2\) (\(x=s\)または\(x=t\)) | \(0\) (\(x=0\)) |
| 最小値 | \(0\) (\(x=0\)) | \(s^2\) (\(x=s\)または\(x=t\)) |
| グラフ |
 下に凸の放物線の最大値と最小値(\(x\)の取り得る値範囲に頂点を含む場合；特に頂点の\(x\)座標と定義域の中点が一致する場合) |
 下に凸の放物線の最大値と最小値(\(x\)の取り得る値範囲に頂点を含む場合；特に頂点の\(x\)座標と定義域の中点が一致する場合) |
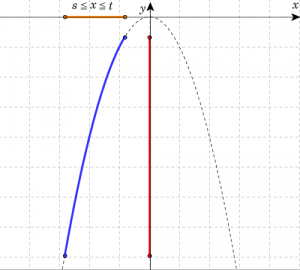
| \(\frac{t+s}{2}>0\)のとき （\(x\)の取り得る値範囲に頂点を含む場合) | ||
| \(a\)の値 | \( a>0 \) | \( a<0 \) |
| 最大値 | \(t^2\) (\(x=t\)) | \(0\) (\(x=0\)) |
| 最小値 | \(0\) (\(x=0\)) | \(s^2\) (\(x=s\)) |
| グラフ |
 下に凸の放物線の最大値と最小値(\(x\)の取り得る値範囲に頂点を含む場合) |
 下に凸の放物線の最大値と最小値(\(x\)の取り得る値範囲に頂点を含む場合) |
| \( s \geqq 0 \)のとき（\(x\)の取り得る値が正の場合） | ||
| \(a\)の値 | \( a>0 \) | \( a<0 \) |
| 最大値 | \(t^2\) (\(x=t\)) | \(s^2\) (\(x=s\)) |
| 最小値 | \(s^2\) (\(x=s\)) | \(t^2\) (\(x=t\)) |
| グラフ |
 下に凸の放物線の最大値と最小値(xの取り得る値が正の場合) |
 上に凸の放物線の最大値と最小値(xの取り得る値が正の場合) |
コメントを残す
コメントを投稿するにはログインしてください。