2012/08/12 - 
数学 
No Comments
数学 No Comments ともなって変わる量
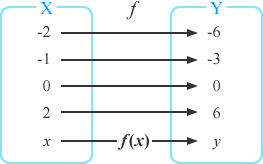
次のような、XとYの対応 \(f\) を考える．
図．ともなって変わる量
XとYはどの\( f \) ような対応になっているか考えてみよう．
Xの中の \(x\) は \(f\) によって \(y\) に対応している．このことを、
\[ y=f(x) \]
と表す．
では，\( f \) にはどのような機能(Function)があるのか？
図を見ると、「2倍する」という機能だといえる．
だから、\( x \) は \( f \) という機能によって、2倍され\( 2x \) となるので、
だから、\( x \) は \( f \) という機能によって、2倍され\( 2x \) となるので、
\[ f(x) = 2x \]
となる (→参照 )． また、\( y = f(x) \) だから
\begin{eqnarray*}
y &=& f(x) \\
&=& 2x
\end{eqnarray*}
即ち，
\[ y=2x \]
と表すことができる．